摘要：利用有限元模型对叶轮模态进行了计算,判断分析了各阶模态振型对气动噪声的影响程度 , 求解中利用了ANSYS 的模态循环对称功能 , 同时分析了旋转软化、应力强化对叶轮真实运转状况下模态频率的影响。
Modal Simulation of Axial Fan Blade and The Effect of That on Aerodynamic Noise
Abstract:Calculation is carried out on impeller modal using the finite element model.Ｔhe effect of modal vibration in various stage on aerodynamic noise is judged and analyzed ,the effect of rotating softness and stress intensification on the modal frequency under the impeller in real operation condition is also analyzed at the same time.
一、引言

　　轴流通风机当其叶片较薄以及过度前掠,重心偏离叶根截面中心时,较高转速造成的离心力和不稳定进气流造成的叶片升力的变化,很容易激发叶片振动。同时由于流固耦合,还可能造成叶片的驰振 ,使叶片提前疲劳损坏,降低风机效率,并产生较大的气动噪声。

　　在叶轮设计时有必要对其振动模态进行计算,但叶片叶身曲面复杂,用经典理论无法求解 ,因此必须借用有限元模型来计算。ANSYS 是当今比较有名的有限元分析软件之一,具有多种物理场的求解功能 , 可以很方便地进行模态分析;大型 CAD 系统软件 UniGraphics 具有丰富的曲面造型功能 , 非常适合于叶轮等具有复杂曲面实体的造型,建好的实体模型导入ANSYS 即可进行模态分析。

二、叶轮 CAD 模型建立和接口导入

1. 叶轮基本参数

　　轴流通风机为整体注塑 ABS 塑料叶轮, 叶片数为4,叶片较宽,叶片呈前掠状。工作转速为 860 r/min,轮毂直径为0.147m,叶轮外径为0.42m 。

2. 几何模型建立

　　通过三坐标测量仪测量得到叶片表面型值点 , 将点阵连接成曲面 , 并利用软件 U G 的曲面剪裁和缝合功能 , 将叶片的曲面连接起来。一旦所有曲面被缝合就自动生成以各曲面为边界的实体。
　　叶轮为循环对称结构 , 为加快有限元分析过程 , 利用 ANSYS 的循环对称分析功能 , 对一个90 °基本扇区进行求解。建模时使全局坐标系的Z 轴与叶轮旋转轴线对应 , 建立完整叶轮模型,然后用过轮毂轴线两个相互夹角为 90 °的两个平面切出 1/4 的叶轮模型 (图 1) 。

3. 导入几何模型

　　能够将UG模型导入ANSYS 的方法有 3 种,其中基于直接的模型数据交换的两种是:一是通过标准的数据接口将 CAD 模型数据转入分析系统;另外是通过ANSYS为UG提供的专用接口直接读入UG的prt 文件;第三种借助UG的GFEMFEA。
　　 这里采取第二种方法 , 在功能菜单中点击File → Import → U G, 再选取零件文件即可。

三、预处理和求解

1. 输入材料物理参数

　　输入ABS材料的物理性能参数:密度为1.2×10-6 g/mm3 ,弹性模量为2.3MPa,泊松比为0.38。

2. 选择单元类型

　　叶轮表面为变厚度复杂曲面 , 选用 10 节点的四面体单元 solid92 , 该单元采用二次位移模式 , 非常适合对形状不规则的实体划分有限元模型。
为了对基本扇区的两个间隔相对 90 °的轮毂的剖面划分网格 , 还选择了一种二维单元:MESH200 单元 , 并设定单元形状参数为“ triangle　with 6 nodes ” (MESH200 单元是专门用来划分网格 , 提供网格占位功能 , 不参加单元运算 ) 。

3. 划分网格

　　先用 MESH200 三角形平面单元划分轮毂上的两个剖面的一个面上的网格 , 然后通过MSHCOPY 命令将该面上的网格拷贝到另外一个剖面上 ( 完成后的网格单元如图 2) 。 对整个模型用 solid92 单元分网格(完成后的网格单元如图 3) 。

4. 边界条件加载

　　叶轮通过轮毂的轴心线装配在电机轴线上 , 叶轮除转动外 , 其它运动都被限制。所以使轮毂圆柱装配面的有限元节点 X , Z 方向的自由度得到约束 ( 在全局柱面坐标系中 ) 。
有限单元的节点都有一个坐标系与载荷方向对应 , 在通常情况下节点坐标系与全局迪卡尔坐标系对应 , 必须首先用 NROTAT 命令转换节点坐标到柱面坐标系中 , 然后再在节点上加载位移约束。

5. 循环对称处理

　　循环对称模态求解是 ANSYS 对循环对称结构提供的一种特殊简化模态求解方法 , 在求解前有一些特殊的预处理。
　　首先 , 需要选择叶轮上下两个剖面上的节点并建立两个组集 , 取名为“Low”和“High”。其次运行 CYCGEN 的宏在基本扇区上建立第二个扇区 , 模态分析就是通过这两个扇区完成的 , 如果不带参数运行这个命令 , 它将内部耦合和约束方程也拷贝到第二个扇区上 ; 如果运行 CYCGEN ‘ , LOAD ’的命令 , 则会把负载也拷贝到第二个扇区上。这里运行 CYCGEN,‘LOAD’。

6. 求解

　　选用 Block Lanczos 为求解方法 , 设置求解频率范围为 20Hz 到 200Hz 。对于求解循环对称模态 ,ANSYS 也提供了专用的求解宏指令(不可直接用 solve 命令),该指令格式为：
CYCSOL , NDMIN , NDMAX , NSECTOR , LOW
　　各参数含义如下 :
　　NDMIN、NDMAX: 计算的上下节径范围, NDMIN 最小为0 ,NDMAX 对偶数最大可取 n/2 , 对奇数最大可取 ( n - 1) / 2 。
　　NSECTOR : 循环对称的扇区数,这里为4。LOW: 较低角度剖面上节点构成的组集名称。
　　该命令对应菜单路径 :Main Menu > Solution > Modal Cyclic Sym。
　　输入CYCSOL ,0 ,2 ,4 ,LOW进行求解。

四、仿真结果与试验结果的对照

　　试验是在叶轮安装状况下通过锤击法进行的 ,支架刚度很大,忽略支架的影响,认为结构在 20～200Hz 范围内的振动模态频率由叶轮决定。试验得到的叶轮模态频率值为 58.17Hz,83. 38Hz ,88. 69Hz ,154. 8Hz ;仿真得到的模态频率值约为 62Hz、80Hz、88Hz 和152. 2Hz。试验检测得出的频率与仿真结果对应关系较好,因此相互得到了验证。由于振型试验比较复杂 ,所以没有进一步作振型试验,后面将利用仿真的数据来观察振型。

五、考虑预应力和旋转软化

　　在真实状况下叶轮是运动的 ,由于离心力和气动载荷的影响 ,叶轮产生拉伸变形,模态有可能与静止状况有很大不同 ,所以必须予以考虑。
影响旋转件频率变化的一种原因是由于离心力对叶片运动产生的预应力的影响 ,造成了叶轮刚度的增大 ,使运行状况下模态频率升高。

　　忽略弹簧变形对质量块向心加速度的影响 ,建立如下平衡方程:
　　　　kx = M^_ωs２ｒ　　　　　　　　　 （１）
式中　k ———弹簧刚度
　　　x ———离开平衡位置的距离
　　　ω_s ———旋转角速度
　　　r ———质点自由位置相对于转轴的半径
　　但是如果弹簧刚度不够 ,同时旋转速度又很大 ,由于离心力的影响使弹簧产生较大位移,而该位移同时又使质点离心运动的半径加大,这时的平衡方程写为：
　　　　kx=M^_ωs２(r + x) 　　　　　　　( 2 )
　　 如果仍然用 (1) 式的形式表示的话,其平衡方程可以写为：
　　　　(k-M^_ωs２)x=M^_ωs２r
　　施加如图 4 所表示载荷时,其振动方程可写为：
　　　　Mx-(k-M^_ωs２)x=f(t)　　　　　
　　因此刚度由 k 变为(k-M^_ωs２),即相当于旋转软化作用 ,旋转速度越高,旋转物体密度越大 ,这种软化作用也就越明显。 应力刚化使模态频率升高 ,旋转软化使模态频率偏低 ,通常应力刚化的作用偏大,所以同时考虑两种因素影响 ,使运转状况下模态频率比静止状况下模态频率偏高。

　　为了获得真实状况与静止状况下模态的差别 ,又进行了一次模态有限元分析,步骤是在三、四步骤后给叶轮施加一个转动角速度,打开预应力开关 ,选择分析类型为静应力分析,并进行一次静应力分析。然后选择分析类型为模态分析 ,并保证预应力开关为打开状态,同时打开旋转软化选项 ,下面同三、五以后的步骤。

　　计算结果各振型对应模态频率变化不到1Hz ,因此该叶轮可以采用静止状况下的模态来代替运动状态下的模态 ,从考虑问题的周全性上考虑 ,对应力刚化、旋转软化验证是必要的。

六、振型和对气动噪声影响的分析

　　为了观察振型 ,用命令Expand 并输入参数4 扩展成整个叶轮以观察振型(菜单路径:Main Menu > General Postprocessing > Expand sector) 。
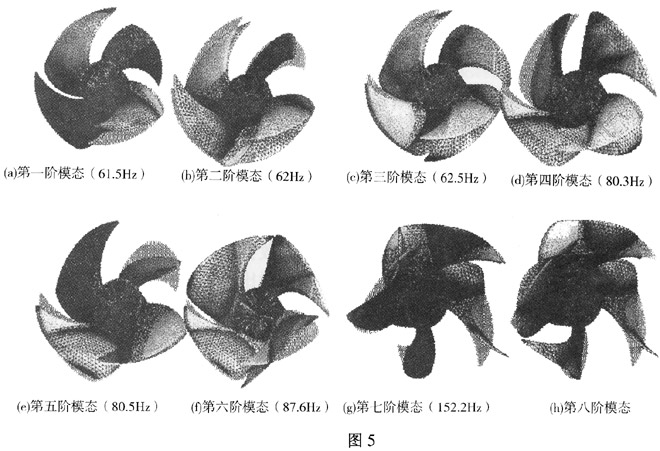
(1) 一阶振动频率为61.5Hz ,叶片表现为沿径向扭摆 ,变形最大位置在叶根处,整个叶轮振型表现为 1、3叶片摆动时,2、4不动,1、3叶片反向扭摆 (如图5a) 。

(2)二阶振动频率为62Hz,叶片表现为沿径向线扭摆,变形最大位置在叶根处,整个叶轮振型表现为1 、3叶片向前扭摆,2、4叶片向后扭摆(如图5b) 。

(3) 三阶振动频率为62.5Hz ,叶片表现为沿径向线扭摆,变形最大位置在叶根处,整个叶轮振型表现为 4 个叶片以相同形式同向扭摆(如图5c) 。

(4) 四阶振动频率为80.3Hz ,叶片仍然表现为沿径向线扭摆 ,但叶片型面上有弯曲现象出现 ,弯曲最大现象出现在较大叶片半径处,整个叶轮振型表现为1、3叶片向前扭摆,2、4叶片向后扭摆(如图5d)。

(5) 五阶振动频率为80.5Hz ,叶片表现为沿径向线扭摆 ,叶片型面上有弯曲现象出现,弯曲最大现象出现在较大叶片半径处 ,整个叶轮振型表现为1、3叶片反向扭摆,2、4不动(如图5e) 。

(6) 六阶振动频率为87.6Hz ,叶片表现为沿径向线扭摆 ,叶片型面上有弯曲现象出现,弯曲最大现象出现在较大叶片半径处 ,整个叶轮振型表现为 4 个叶片以相同形式同向扭摆(如图5f) 。

(7) 七阶振动频率为152.2Hz,1、3叶片的运动形式以叶片型面上的弯曲波为主 ,弯曲波有两条节线 ,且弯曲波最严重发生在叶片外周处,1、3叶片运动形式相差180°相位;2、4叶片基本不动 ,但在前掠的叶尖处有少量翘曲;对面的叶片变化相位差 180°(如图5g) 。

(8) 八阶振动频率为152.6Hz ,叶片表现4个叶片型面上都出现弯曲波 ,且整个叶轮相对的两个叶片振动情况相同 ,而相邻的叶片振动情况相差 180°相位(如图5h) 。

　　可以看出叶轮模态振动形式主要是由 4 个叶片周向不同振动组合形式 ,造成这种原因主要是前掠叶片刚度远小于轮毂的刚度 ,即叶片“软” ,而轮毂“硬”;叶片低频振型主要以叶片整体扭摆为主 ,而高频主要以叶片弯曲波为主。从对噪声的影响来看认为前六阶振型影响较大 ,因为由于它的摆对流场有较大影响,造成了叶片进气攻角的变化 ,从而形成叶片表面升力的波动 ,最严重的情况会产生驰振,产生很大气动噪声和效率较大的降低。

七、结论

　　通过有限元对叶轮模态进行了模态分析,考虑了旋转软化、应力强化对叶轮真实运行状况下模态频率的影响,发现与静止状态差别不大 ,同时分析结果与试验吻合较好。通过振型分析 ,认为较低频率的前六阶振动对气动噪声影响较大 ,为设计低噪声风机提供了借鉴。

　　下一步将计算叶轮流场 ,得到叶片流场受力并对叶轮作谐波分析 ,通过气动声学公式预测噪声的大小 ,以期望获得叶轮振动对气动噪声的具体量值。

参考文献

[1] 李庆宜.通风机.机械工业出版社,1981.
[2] 沃德·海伦等.白化同等译.模态分析理论与实验.北京理工大学出版社,2001.